In the January/February Skeptical Inquirer Professor Jim Enright makes a damning analysis of the extensive test of dowsers which was carried out in Germany in the late 1980's. It occurred to me that any computer-proficient skeptic could carry out a control experiment. (Hint, this would make a neat science fair project.)
There's no need to hunt out hundreds of dowsers and spend time and money testing them. My dowsing experiment needed just me and my computer to replicate the entire German test. I tested 500 dowsers who are guaranteed to have no dowsing ability whatsoever, indeed they don't even exist. My aim was to see if any of them would achieve "significant" results.
In my simulation the target water pipe is given a random position on a scale from 0 to 9.9 meters. My phantom dowsers make a completely random selection, also from 0 to 9.9 meters, of where they think the pipe is. Each dowser makes ten attempts.
As Enright suggests, there are at least two ways of analyzing the results. One measure is the sum of the absolute values of the miss distances. This makes a miss by two meters twice as bad as a miss by one meter. The other is the Root Mean Square (RMS) measurement where a miss by two meters is four times as bad as a miss by one meter. The latter measurement is easily converted into the standard deviation, the measure universally used in science to describe how widely experimental results are spread around their mean value. Being mainly interested in how close the results came to perfection, rather than in how consistently they were wrong, I took the RMS error as my criterion, not the standard deviation. The difference is small and the same dowser came out best.
I used two digit random numbers to place my pipes and make the divinations. Since computer generated random numbers are, or were, notoriously non-random, I used the first 20,000 digits of the fractional part of pi. (From the list of 1.25 million digits published by Project Gutenberg®.) The digits of pi have the advantage of being both random and reproducible, should anyone wish to check my results.
On testing each dowser the program retained the best result found so far. As it happens, number 500, the last dowser tested, achieved the best results. (I checked rather carefully to be sure this was not an artifact of the program.) He (or she) had a mean absolute miss distance of 1.43 m, a mean error of 0.47m and a standard deviation of 1.82 m. The RMS error of the ten trials was 1.79 m.
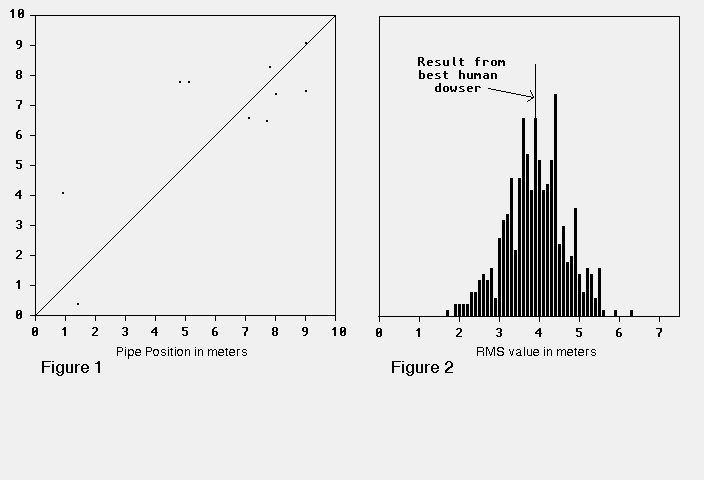
This result is somewhat better than that which Enright categorizes as "Modest Skill." Indeed, from Figure 1, a plot of estimate versus pipe position, it seems that my phantom "best dowser" shows definite dowsing ability.
My phantom dowser did considerably better than the famed "real" dowser #99. Results supplied by Jim Enright (from his Figure 2b) show that dowser's RMS error to be 3.96 m. (SD, 3.64m. Mean, 1.93 m.) A completely random selection of the pipe and guess positions gives an RMS error of 4.08 m. Any real dowser should show a much lower figure.
Figure 2 plots the RMS errors achieved by all 500 of my phantom dowsers. No less than 235 of them did better than the best German dowser.
By the normal scientific criterion for goodness of result the "best" German dowser did very badly, having an RMS error hardly better than random guessing. One thus wonders what led him to be selected as worthy of note.
Presumably the impact of five near hits (see Enright's Figure 2) distracted the experimenters from the five outright misses. In science we don't work this way, we take all our results into account. To do otherwise is called "data mining," a process which all too often results in finding fool's gold. The claim that the German experiments show evidence for the validity of dowsing is not only absurdly optimistic, it reveals a startling ignorance of statistical analysis.
The author wishes to thank Professor Enright and PhACT member Ed Gracely for their helpful comments on an earlier version of this report.